读完本篇文章你的收获:

1.PID三个参数基本概念

2.了解如何调节PID

3.认识-一个钻研技术的博主

先上效果图:

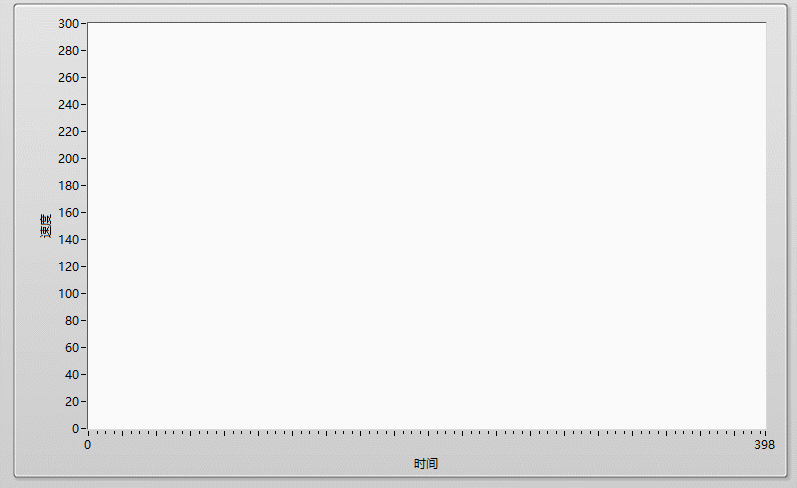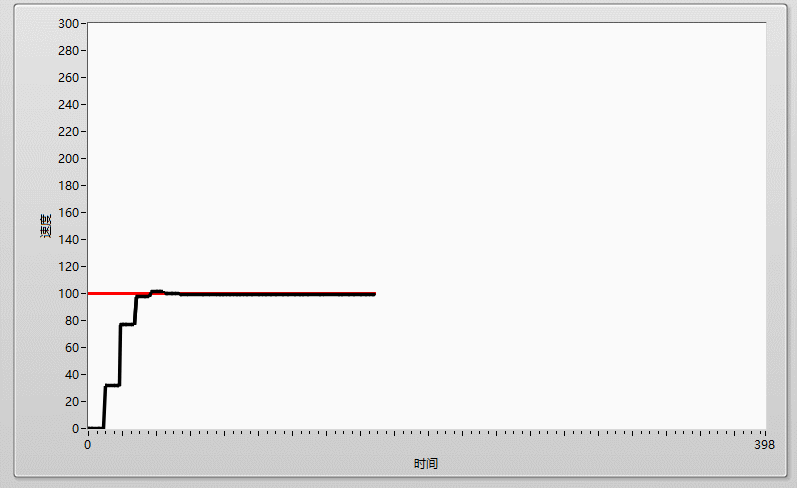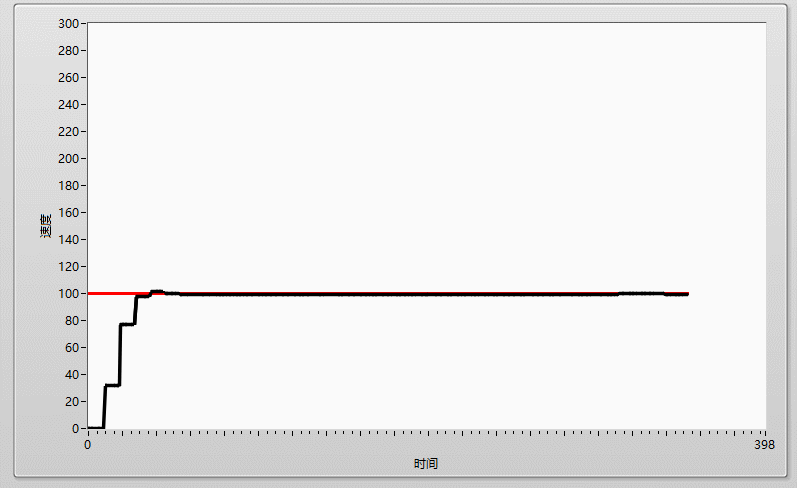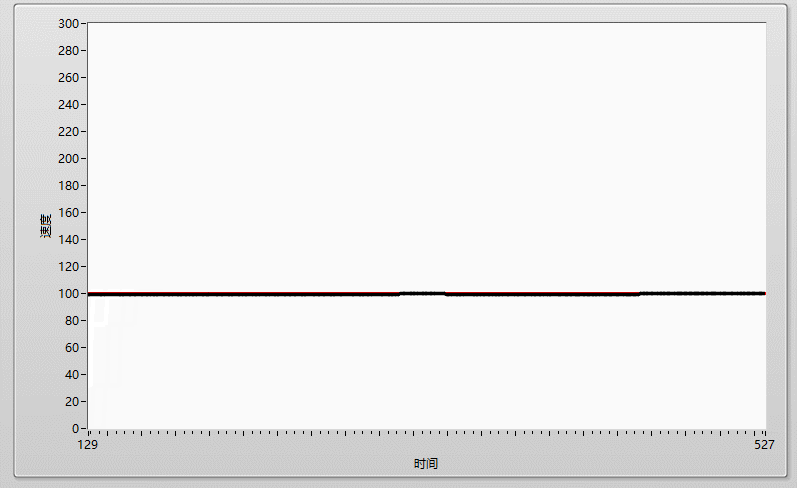
一、什么是PID

在工程中，如果我们要用单片机做一个温控系统，期统组成-般如下: -个采集温度的ADC, -一个输出温度的加

热头以及一一个用于运行控制算法的单片机，如果我们要维持温度为100度,在不加任何控制算法的情况下，我们可

以通过简单的阈值判断法来控制温度，-个if判断语句, 当采集到的温度大于100时，单片机控制加热头关闭，当采

集的温度小于100度时，单片机则控制加热头开启,简单粗暴，但这样的控制方法，最终所展示出来的温度曲线是

极其不稳定的，他会由于控制器件的灵敏程度、加热头的性能等等原因，导致最终的温度曲线会在目标周围震荡,

达不到理想的控制效果，就像下图:实际曲线(黑线)在目标曲线(红线)周围抖动

那如何才能维持实际曲线与目标曲线贴合,达到一一个稳定的控制效果呢?

这里就引入了PID控制算法的概念, PID是Proportion Integration Differentiation 的缩写，实际上他就是一个公式,

此例项(Proportion) ,积分项(Integration) ,微分项(Differentiation) 三个部分组成，具体形式就是下

面的公式:

其中err(t)就是当前值和目标值的误差, PID的公式就是对这个误差分别进行比例、积分、微分处理后叠加输出，因.

为此例计算、积分计算、 微分计算 在数学公式上的计算定义不同,所以对应的项的输出特性和输入特性也有着不

同，具体解释如下:

1.比例系数

比例控制系数,实际上就是先简单的定义输入与输出的线性关系，假如我们输出控制量的值得范围在100-1000,

输入的err误差范围却在0.001-0.1;当误差为0. 1的时候输出量需要到达到1000,这时我们就需要通过比例系数来构

建输入与输出的线性关系

2.积分系数

上一点我们分析了比例系数的含义，有小伙伴可能会好奇,比例系数加上后的效果其实和阈值判断原理没什么区

别，确实是这样,只用上比例系数的效果和阈值判断没什么区别，但别忘了，PID后面还有和D两项，中项的理

解我们可以从积分的含义来理解，积分可以理解为在坐标平面上，由曲线、直线以及轴围成的曲形的面积值，这个

曲线就是err(t)的函数，这个积分面积值就是代表过去一段时间的误差累计值, 我们把这个累计值乘以系数进行变

换后,叠加到输出上，就可以一定程度上消除历史误差对当前实际曲线的影响，提高系统的稳定性

3.微分系数

微分的数学理解可以理解为当前误差曲线的斜率，他可以用来预测当前曲线的未来走势，对微分项的值进行处理后

珈，就可以预测当前值的未来趋势，提高系统对未来变化反应能力

二、PID调节方式

通过.上一小节的分析,我们对PID的三个项有了-个简单的理解，文字上的描述还是太抽象了，我以一个小车调

速系统来做进一步讲解， 结合实际现象来分析PID三个参数的实际作用,以及如何调这三个参数，用到的实验平台

如下

1.平衡小之家的主控板及电机

2.自己编写的调试上位机.

控制系统图片: 

上位机界面:

我们在使用PID的时候，单独织使用一个参数是没有意义的至少使用两个参数,瓶P (比例项)是必须要有的,

虽然PID有三个参数,但大多数情况下PID三个参数并不是都使用上的，-般会其中两个来组合使用,比如PI组合

用于追求稳定的系统，PD组合用于追求快速响应的系统，当然PID用于即追求稳定又追求快速响应的系统，但是实

际上PID参数越多越难调,而且许多情况下两个参数的效果已经足够了，所以我一般根据情况使用前两个，下面对

这几个系统都做一个分析

1.PI系统调节

调节PI系统的第一步就是 先调节P，由小到大依次调节，P的值可以很明显的在输出曲线体现出来,比如哦先给P=

0.05，系统反应如下，当P过小时，曲线呈现缓慢上升，且最终值会明显低于目标值

当我们加大P到0.15时,我们可以看到实际曲线很快的接近目标值,但因为只有单纯P控制,所以有较大的过冲

(过冲就是实际值达到目标值时刹不住车,冲出去了)，但在他稳定的时候，实际曲线基本接近目标曲线

如果P再增大到0.25，可以看到，实际曲线需要震荡很久才会达到稳定目标线，但在稳定后基本和目标线保持一致

如果P过大，整个系统就会不受控,实际曲线不会收敛到目标曲线位置，出现等幅震荡，比如P=0.45时

在调节PI系统时，P的选取-般有两种情况

1. P偏小-点，稳定时，实际值在目标值之下，- -直存在误差,这时再从开始, - -直加大I, 消除稳定时的误差,

这种情况下的最终稳定曲线会- -直保持在目标曲线之下，达到比较稳定的调节效果，不会有过冲(无过冲，稳

定! )

2. P大-点，在第一次到达目标值的时候有一 定的过冲,但之后就会稳定，其与第-种相比反应速度更快! (有过

冲，但他快! )

下面展示第一种PI控制方式， 选取P=0.5 (偏小)时，再用消除稳定时的稳态误差,达到稳定的效果:

|积分的值这里我展示了三个，分别为较小，刚好，和较大时的实际曲线,用来做对比!

P=0.5, I=0.00005, l选取较小，可以看到相对于单纯的P=0.5,稳定误差有一定消除， 但消除程度不够!

在加大到0.0刚刚子的时候,实际曲线和目标曲线基本重合! ! !

当过大取0.002时，因为累计误差比过大，就会出现抖动现象，难以收敛

上面就是第一种PI调节情况，虽然PI系统平衡过程很稳定，但到达目标位置的反应速度较慢，有的时候为了提高反

馈速度，适当的提高P，允许有一定的过冲， 比如我取P=0.07,对应的取0.0001时，波形如下，该系统允许一定的

过冲,但可以更快的到达目标点后再趋于稳定，这就是第二种PI系统的调节方式

以上基本就是PI系统的调节过程了，下面我讲一 下PD系统的调节过程

2.PD系统调节

由-开始的概念我们可以知道，与1的不同点在于，是计算累计误差,而D则是计算未来趋势,因此PD系统的反应

速度更快，相对于PI系统会更快的到达目标位置附近,其调节方式首先还是调节P,这里我们根据PI中P的调节结

果，调节P到此大的位置,出现-定的过冲，这里取P=0.15,不加D的时候图形如下:

从图像可以看出: P=0.15在开始时过冲严重，所以加上一个D来减小过冲幅度，D的选取和的选取一样,从0慢慢

增加，观看效果确定合适的点，下面一 -张图的D=1.5是我试出来比较合适的点， 我们可以看到加上合适的D之后,

实际曲线到达目标位置的时间更短，过冲幅度也降低了- -些,但是这里效果不是很明显，要原因是我这里使用的

是小车轮子来做的速度PID,而PD的应用场合主要是大惯性系统中，这里的应用场景不适合，但也能看出一-定效果

如果D调节的过大之后，反倒会放大系统趋势的影响，使系统出现震荡,难以稳定,如下D=5

3.PID系统调节

正积有一的罐节方过标 正和事-下口系的调节方式 首先盼拔按驴系续进行闻书 先脚在

调,让系统有一定的过冲后达到稳定，

如下图:

在出现了上面的PI波形之后，下面就开始调节D,慢慢增加D,将过冲补偿掉,直到系统稳定,最终效果如下图,

PID系统就基本调节完成了